1 kristályrács
A kristályos rács lehet meghatározni kaksovokupnost periodikusan távolságban lévő pont a térben, amely összefüggésbe hozható a központok képező egy kristály atomok vagy molekulák (4.2 ábra). Az a pont, amely található atomok maguk vagy molekula (pontosabban, az a pont, amely körül végre a hő oszcilláció) nazyvayutuzlami rács (4.2 ábra, a). Atomcsoport, amely társítva van minden egyes csomópont a rács (4.2 ábra, b) nazyvaetsyabazisom (ilyen csoportok azonosnak kell lennie az összetétele, hely és orientáció).
A több rács csomópontok valójában - obrazuetprostranstvennuyu absztrakt halmaza rácspontok (4.2 ábra, a) kristály.
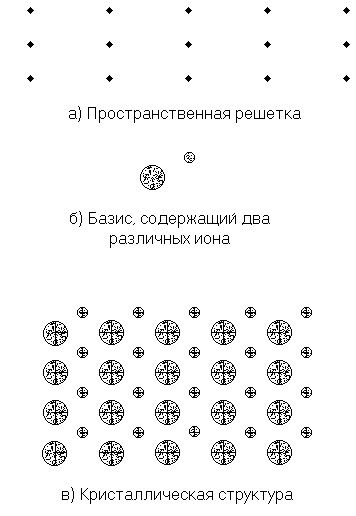
Így a kristályrács - egy térrácshéj egy alapot.
Ábra. 4.2. kristályos szerkezet: a) rácsos csomópontok alkotnak térrácshéj; b) egy csoport alkilcsoport, amely található rácspontjain (bázis); c) a kristályrács, ami egy „sum” a rács és a bázist; Ezen az ábrán a rács csomópontok már nem látható.
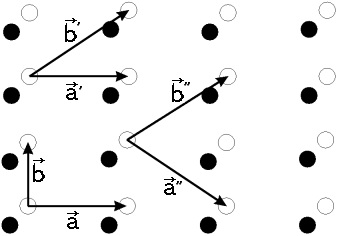
Ábra. 4.3. Vektorok sugároz egy kétdimenziós rács egy alapja két atom (fehér és fekete kör). A választás Ezen vektorok nem egyértelmű (

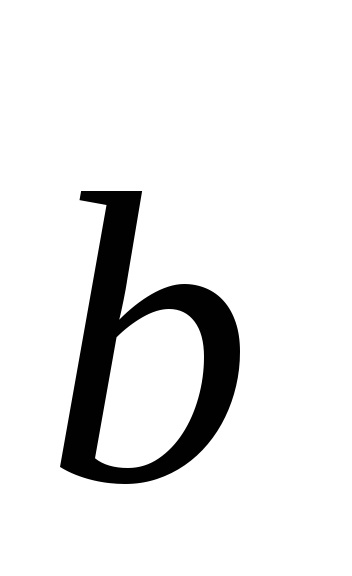

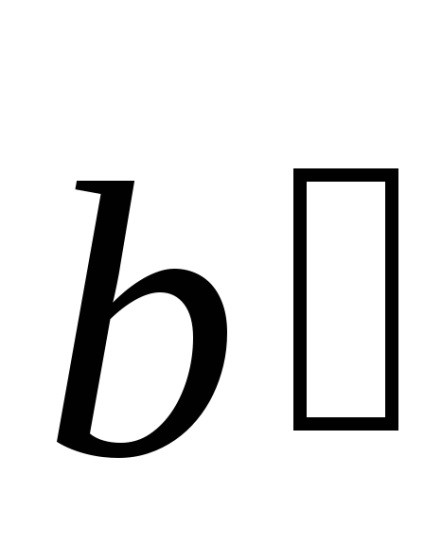



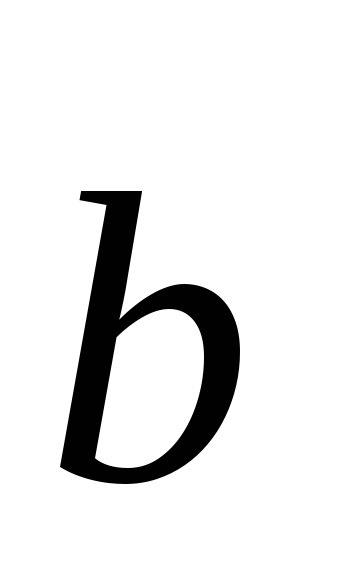

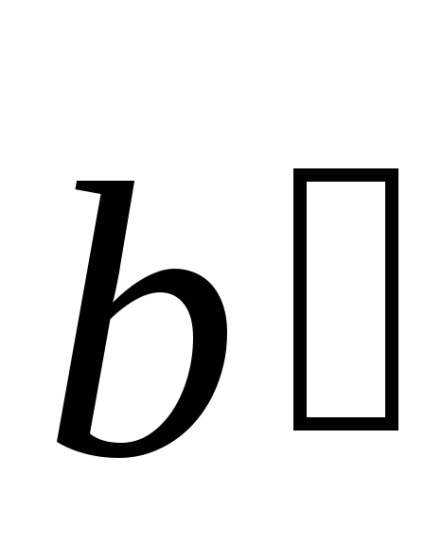


A fogalom a térrácshéj vezette be a francia matematikus és kristályosító Auguste Bravais (1811-1863). Ez különösen hasznos, ha érdekli csak a térbeli periodicitás elrendeződésében atomok a kristály, de nem érdekli annak specifikus kémiai összetétel. Bármely Bravais rács (köszönhetően frekvencia) nem találja a három vektor egy síkban fekvő

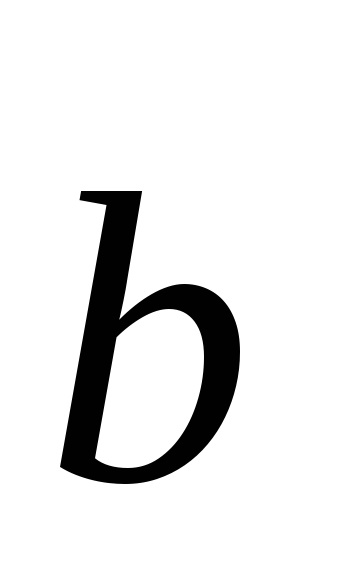
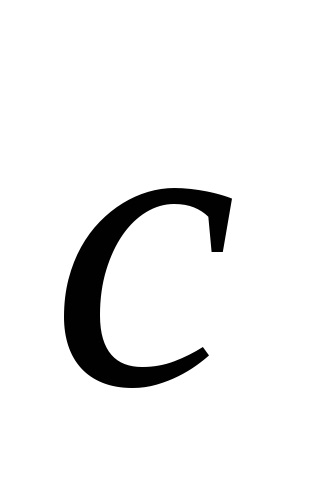
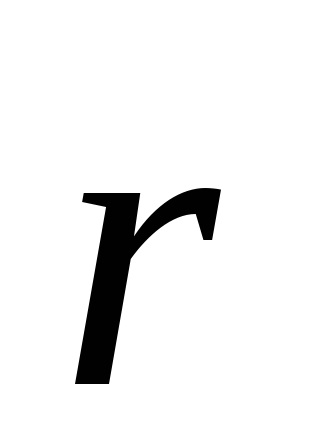
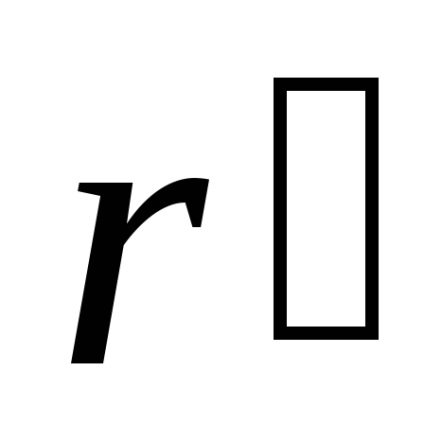
,
ahol m, n ip - tetszőleges egész szám.
Így, az összes pontot (csomópontok) Bravais rácsos egyenértékű ,. E. Van ugyanabban a környezetben. Más szóval, minden csomópont látható ugyanabból a rács mintát.
vektorok

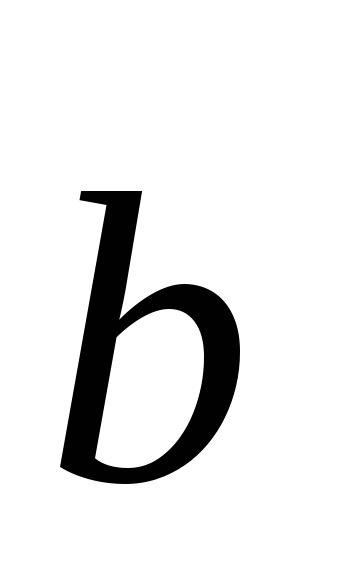
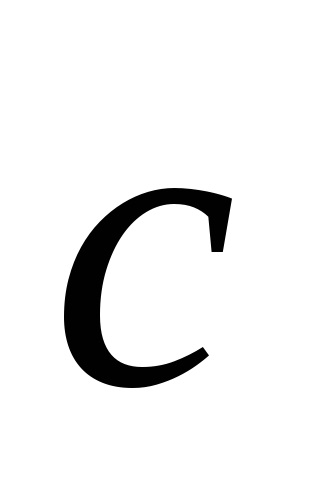
Egyértelmű, hogy a vektorok

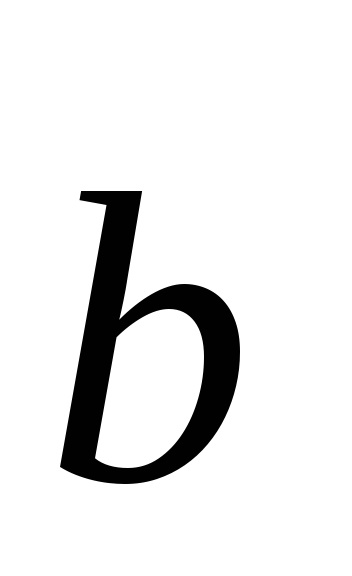
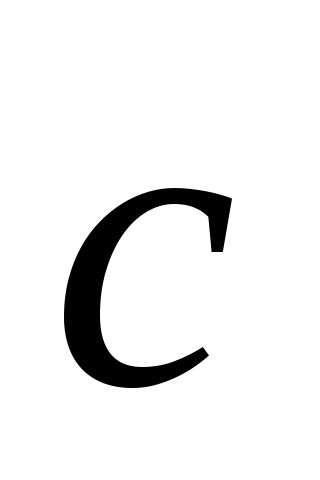

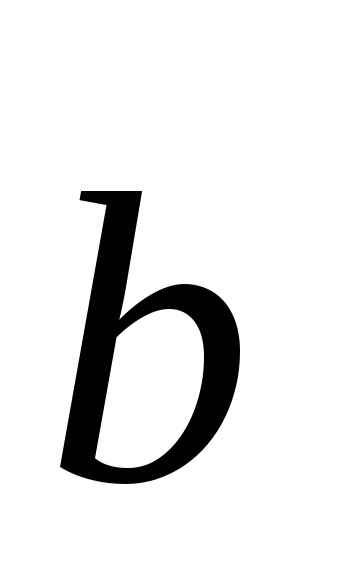
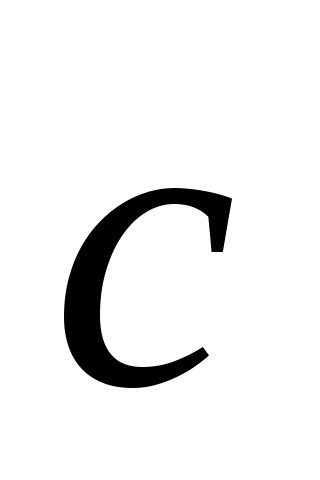
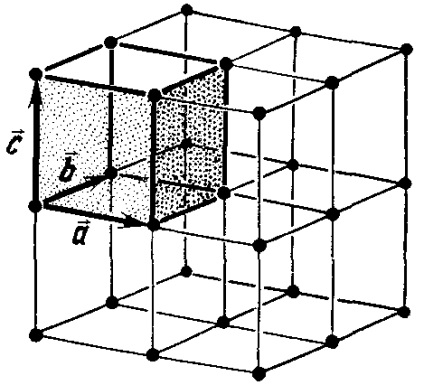
Ábra. 4.4. Alapvető fordítás vektorok

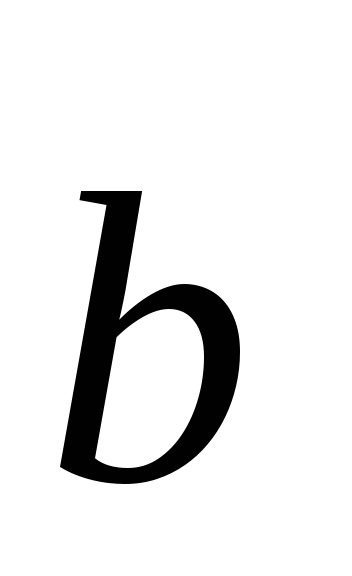
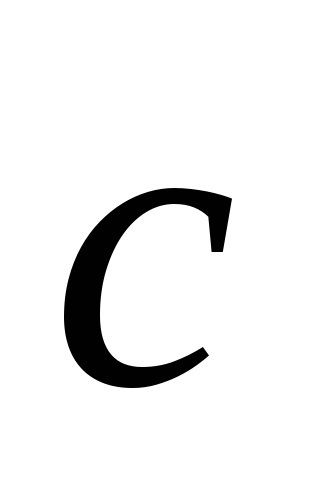
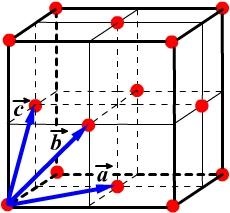
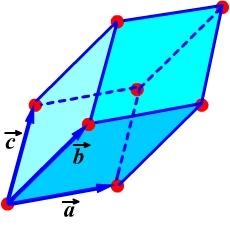
Ábra. 4.5. Az egység (a) és primitív (a) sejt dimenziós Bravais rács. Ábrázol lapcentrált köbös (FCC) rács. Minden ábrán vektorok

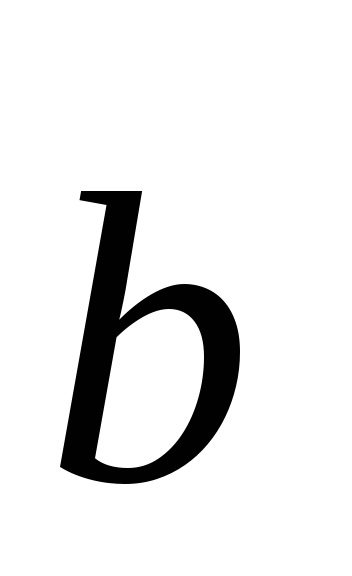
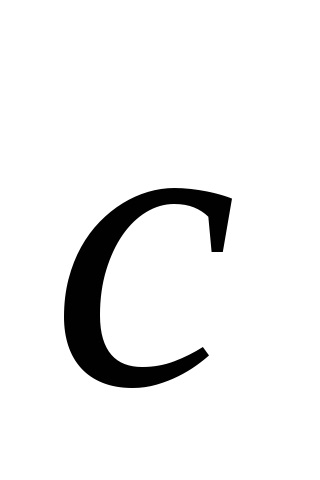
A primitív cellának csupán egyetlen pont a Bravais rács (Fig.4.5, c). Míg mind a nyolc sarkában a paralelepipedon egy rácspont, Minden ilyen ponthoz tartozik egyidejűleg nyolc sejtek, amelyek ponttal szomszédos megfontolás alatt, így az egyik cella 81 / 8 = 1 pont. YacheykiVc primitív által meghatározott térfogatot az alap vektorok kevert termék adások:
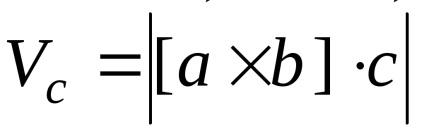
A primitív sejt egy speciális esete az elemi cella. Ebben az esetben, a fő vektorok adások, és így a primitív sejt, is ki lehet választani a különböző módokon. Ábra. 4.3, például, (

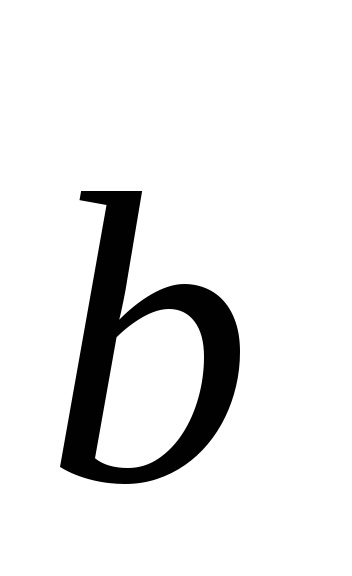

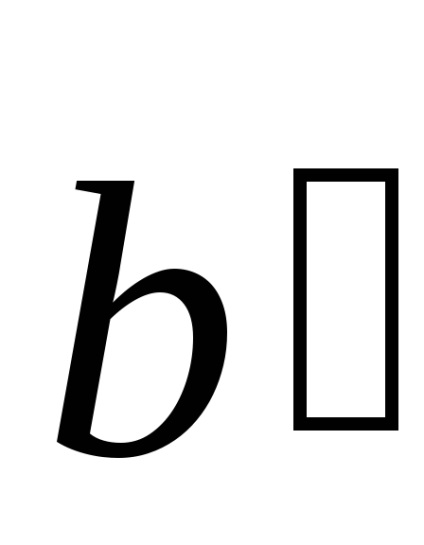


Egy másik lehetőség a választás primitív sejt ábrán látható. 4.6. A sejteket a kiválasztott, oly módon, az úgynevezett a fizika primitív sejt Wigner-Seitz.
Az egyedi jellemzői a kiválasztott egységre, vagy primitív sejt (Fig.4.5, c) általában kell beállítani értékek 6: 3 sejt élek a, b és UC három szög közöttük -, , és . Ezek az értékek nazyvayutparametrami cellában. A oldalhossza az elemi cella, azaz a hossza az alap fordítás vektorok nazyvayutperiodami adásokat.
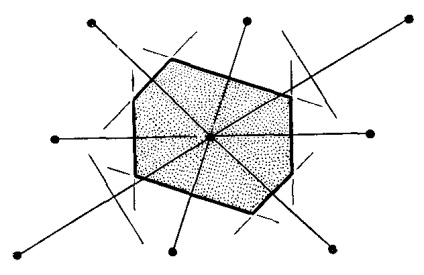
Ábra. 4.6. Primitív sejtek lehet kiválasztani az alábbiak szerint (a): 1), hogy összekötő vonalak egy adott rácspont az összes szomszédos pont; 2) a közepén a merőleges vonalak őket tart egy új sort (abban az esetben, kétdimenziós rács) vagy sík (abban az esetben, háromdimenziós rács). Az így kapott sejt a legkisebb mennyiség, amely csak az egyik rácspont nevezzük primitív sejt Wigner-Seitz. Használata az ilyen sejtek töltik ki az egész teret a kristályrács keresztül, valamint a primitív sejtek ábrán látható. 4.3. Symmetry primitív Wigner-Seitz egybeesik Bravais rácsos szimmetria. Ez látható a példa egy háromdimenziós cellában Vigenra Seitz (a) egy tércentrált köbös központ (BCC) rács (b).
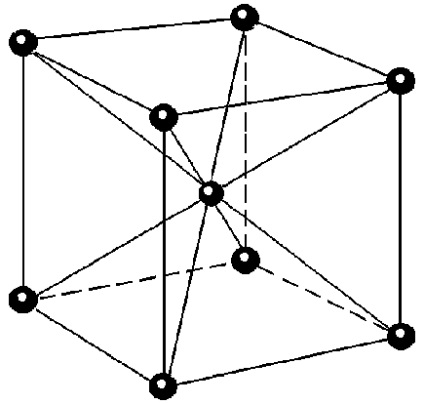
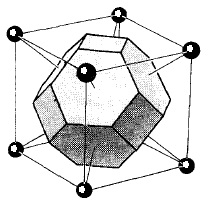
Olyan megfelelő fordítások (eltolódások) a primitív sejt vektorok

A kristályokat Számos fém és inert gázok alapján áll egyetlen atom. De az ismert szervetlen és biokémiai szerkezete, alapján, amely magában foglalja egy ezer vagy több atom.
Ha a kristályrács alapján áll egy atom, a kristályrács egyszerű. Ebben az esetben, az összes atomok a kristály vannak elrendezve Bravais rácsos csomópontok.
Ha alapján épül fel néhány atom, a kristályrács összetett. Ebben az esetben minden egyes atom saját bázis podreshetkaodnotipnyh atomok, azonos Bravais kristályrácsban.
Egy példa a kétdimenziós komplex rács ábrán látható. 4.3. „Fehér” és a „fekete” atomok lehetnek kémiailag azonos, de ezek különböznek a pozíció a kristályrácsban. Az atomok egy kristály azonos típusú, ha azok kémiailag azonosak, és mindegyik látható egy és ugyanazt a képet a kristályrácsban.
Így, hogy „látni” a Bravais rács, szükség van a „látni” csak az azonos típusú atomok. Amikor ez a kristály egy komplex rácsos lehet képzelni kétféleképpen: 1) veszi alapul, és sugározható használatával újból primitív transzlációs vektorok, vagy 2), hogy több, pontosan azonos Bravais rácsok, és behelyezi őket egymással, elhelyezve a csomópontok a megfelelő tömbök az azonos típusú atomok . Kétdimenziós kristály látható. 4.3, például, két egymásba húzott Bravais rácsok, amelyben a csomópontok vannak elrendezve rendre „fehér” és „fekete” atomok.