1-es típusú

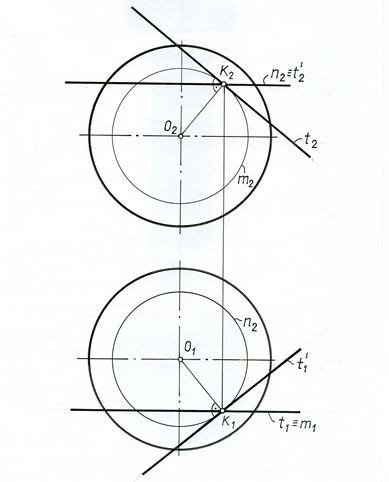
Probléma 1. Construct egy érintő sík a felület egy gömb a K pontot (ábra. 11.2).

Mi választjuk ki a két görbe vonalak ponton áthaladó C. Célszerű, hogy a legtöbb grafikailag egyszerű vonalak - a kör (párhuzamok és meridiánok) - n és m.

Ahhoz, hogy ezeket a két kört egy ponton érintő a huzal, ahol mindegyik síkban a kerületének, vagyis a t abban a függőleges és t „- a vízszintes síkban.

Beépített érintők t és t „és adja meg a kívánt érintősík.

Ebben a feladatban a pont - az érintési pont elliptikus. OK - sugara a normális, hogy az érintőleges sík pontban K. síkban épített merőleges.

Probléma 2 Construct érintő sík felületén forgatás

K. pontjában (ábra. 11.3).

Mivel a vonalak, amelyek meghatározzák a érintősík, hogy két

vonalak, amelyek közül az egyik kör érintőjén - párhuzamot, áthalad a K pontot, a második - az érintő egy meridián áthaladó ugyanazon a ponton.

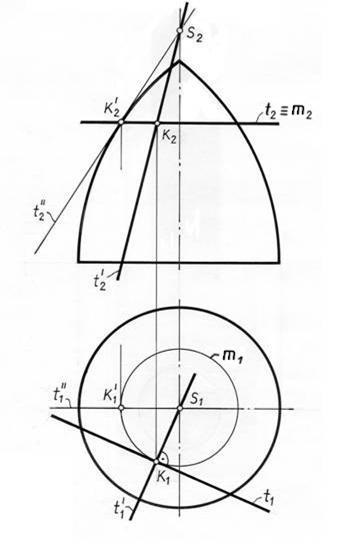
Felhívni a érintő meridián, kapcsolja fel

igazodás a fő meridián és felhívni a T érintő „” 2 azon a ponton,

K'2. fekvő azonos kerülete párhuzamos, mint a K pontot, hogy a kereszteződés a szimmetria tengelye a számadatok azt a pontot S. után ugyanabban a pontban S kerül sor T érintő „2 visszatérése után elfordítható meridián eredeti állapotát. A kivitelezést, csatlakoztassa S2 és K2.

A második T érintő van kialakítva oly módon. Her frontális vetítési t 2 az első vetítési síkja egybeesik a vetülete a kerülete párhuzamos m. A vízszintes vetülete t 1 van kialakítva, mint egy érintő vonal a kerülete a vízszintes vetülete - párhuzamos m1.

Érintő t „és t” és meghatározza a szükséges érintősík.

Vegyük észre, hogy ez a probléma megható K pontot is érintési pont elliptikus.

Probléma 3. Construct érintőlegesen a henger pontban K (ábra. 11.4).

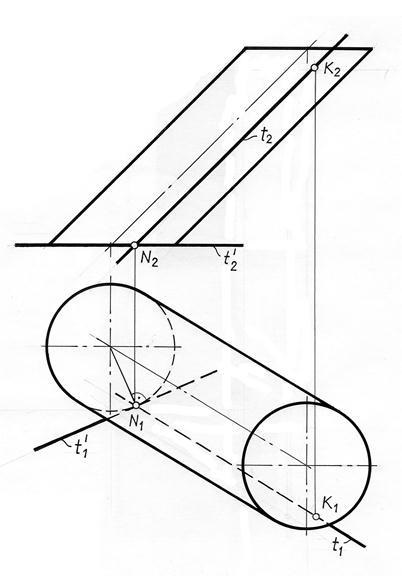
Element érintési síkra a henger alkotó henger lesz t. amely abban rejlik pont K. Ebben a feladatot, az érintési pont K egyike több geometriai parabolikus érintési pontok feküdt egy alkotója a henger. Ezzel első alkotója egybeesik t érintő vonal a felszínre.

A második érintő vonal áthalad a ponton N, ami fekszik az alapja a henger. Ez a pont az a pont, a metszéspont a gép t alkotója a henger bázis.

Beépített tangens vonalak t és t „és a forma egy érintő sík a henger pontjában K.